В треугольнике АВС на сторонах АВ и АС взяты точки K и N так что АК=1/3*AB и AN=2/3*AC....

Формула площади треугольника:

$S=a*b*sin \alpha \alp:2$ , где а и b- стороны треугольника, α- угол между ними.⇒

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

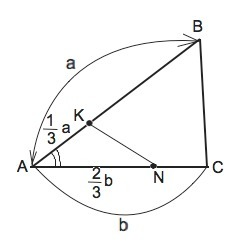
Пусть Ѕ1- площадь Δ АВС, Ѕ2– площадь Δ АКN.

Примем АВ=а, АС=b

Тогда АК=а/3, АN=2b/3

AB•AC=ab

$AK*AN= \frac{a}{3}* \frac{2b}{3}= \frac{2ab}{9}$

$\frac{ S_{1} }{ S_{2} }= \frac{ab}{ \frac{2ab}{9}} = \frac{ab*9}{2ab} = \frac{9}{2}$ ⇒

2S1=9•S2 ⇒

S2=36:9=4 (ед. площади)

В треугольнике АВС ** сторонах АВ и АС взяты точки K и N так что АК=1/3*AB и AN=2/3*AC....

В треугольнике АВС ** сторонах АВ и АС взяты точки K и N так что АК=1/3AB и AN=2/3AC....