Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Противоположные стороны параллелограмма попарно равны.
Признаки:
1) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
2)Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
3) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
1 признак:
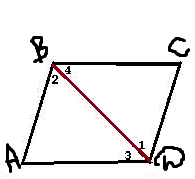
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD. Эти треугольники равны между собой по двум сторонам и углу между ними (BD - общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.