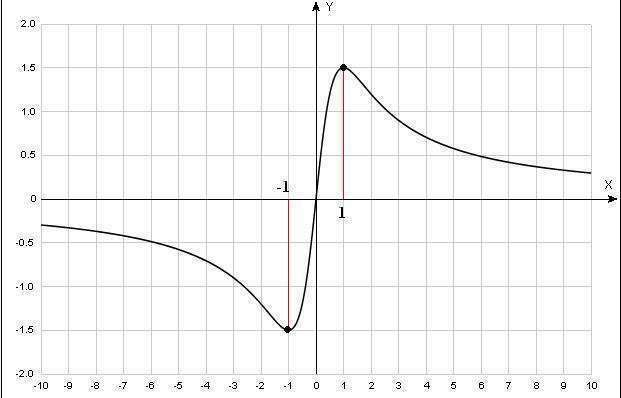
F(x) = (3x)/(1+x^2)
f ' = (3*(1+x^2) - 2x*3x)/(1+x^2)^2 = (3 + 3x^2 - 6x^2)/(1+x^2)^2 = 3*(1 - x^2)/(1+x^2)^2 = 0
1 - x^2 = 0, x^2 = 1, x= +-1
При x∈(-1;1) производная положительная, значит функция возрастает
При x∈(-бесконечность; -1)u(1; +бесконечность) производная отрицательная, значит функция убывает.
x = -1 - минимум
x = 1 - максимум