3.
По
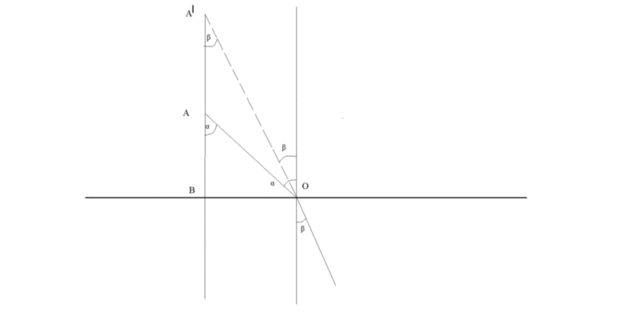
условию задачи A´B = 2.5 м.
Из рисунка видим, что
BO/A´B=tg(β),
аналогично
BO/AB=tg(α)
Отсюда:
A´B/AB = tg(α)/tg(β)
При взгляде вверх, углы малые
и tg примерно
равен sin
A´B/AB = sin(α)/sin(β)
Учтем, что
sin(α)/sin(β)=n
для воды
n=1.33
A´B/AB = 1.33
AB= A´B/1.33
AB=1.88 м
4.
Поскольку при прохождении лучей справедливо утверждение, что
их траектории не меняются при повороте направления, то отношение длины
уменьшенного изображения к длине предмета равно отношению длины увеличенного
изображения к длине предмета.
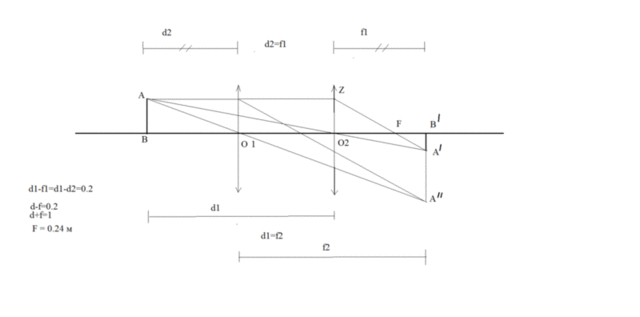
Из
симметрии построения хода лучей можно сделать вывод
d1=f2 и d2=f1,
поэтому справедливо
d-f=0.2
естественно
d+f=1
сложив, получим
2d=1.2
d=0.6
f=0.4
1/f+1/d=1/F
F=0.24 м