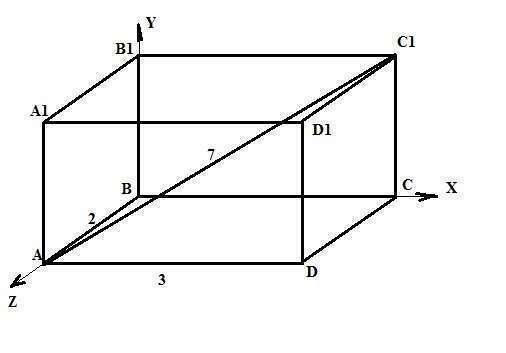
Если не ошибка в условии, то и без решения видно, что угол между АВ и В1С1 равен 90° не зависимо от размеров сторон данного параллелепипеда. Поскольку АВ и В1С1 скрещивающиеся прямые, а угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся. То есть это угол между А1В1(А1В1 параллельна АВ). А он равен 90°, так как параллелепипед прямоугольный.
Но можно и посчитать:
АС=√(4+9)=√13. СС1=√(49-13)=6 (все по Пифагору)
привяжем систему координат к точке В.
Тогда имеем точки с координатами:
А(0;2;0), В(0;0;0), В1(0;0;6) и С1(3;0;6).
Вектор АВ{0;-2;0}, его модуль |AB|=√(0+4+0)=2.
Вектор В1С1{3;0;0}, его модуль |B1C1|=√(9+0+0)=3.
Cosα=(AB*B1C1)/(|AB|*|B1C1|) или
Cosα=(0*3+(-2)*0+0*0)/6 =0. Угол равен arccos0 =90°. Это ответ.
P.S. Все-таки в условии, наверно, ошибка. Но при любых данных угол между любыми скрещивающимися прямыми в данном параллелепипеде можно найти приведенным методом. Надо только правильно определить координаты необходимых точек.