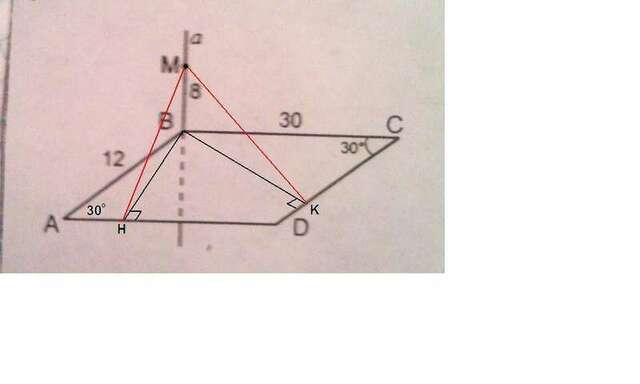
Проведем ВН⊥AD и ВК⊥CD.
ВН и ВК - проекции наклонных МН и МК на плоскость параллелограмма, значит МН⊥AD и МК⊥CD по теореме о трех перпендикулярах.
МН и МК - искомые расстояния.
В параллелограмме противолежащие углы равны, значит ∠А = ∠С = 30°.
ΔАВН: ∠АНВ = 90°, ∠ВАН = 30°, ⇒ ВН = АВ/2 = 6 как катет, лежащий напротив угла в 30°.
ΔСВК: ∠СКВ = 90°, ∠ВСК = 30°, ⇒ ВК = ВС/2 = 15 как катет, лежащий напротив угла в 30°.
Из прямоугольного треугольника МВН по теореме Пифагора:
МН = √(МВ² + ВН²) = √(64 + 36) = √100 = 10
Из прямоугольного треугольника МВК по теореме Пифагора:
МК = √(МВ² + ВК²) = √(64 + 225) = √289 = 17