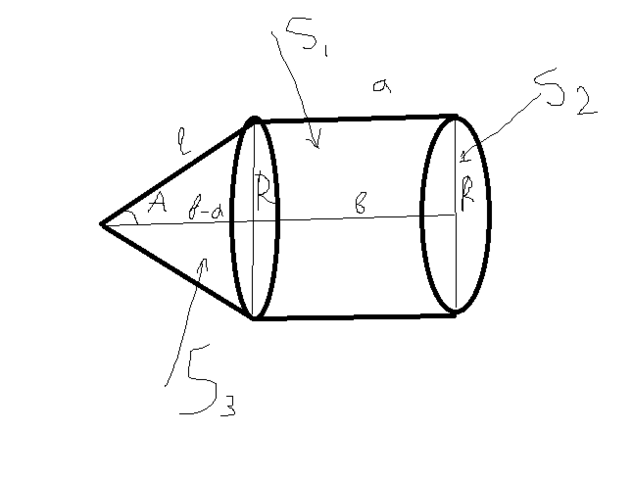
при вращении образуется фигура, состоящая из цилиндра и конуса и площадь будет равна сумме боковой поверхности конуса, боковой поверхности цилиндра и площади круга, образованного вращением прямоугольной стороны трапеции.
1)S1= 2ПRa
R= (b-a)tgA
S1= 2Пa(b-a)tgA
2)S2=ПR^2
S2= П* ((b-a)tgA)^2
3)S3=ПRl
l=(a-b)/CosA
S3=П* (b-a)tgA* (b-a)/CosA
S=S1+S2+S3 = 2Пa(b-a)tgA+ П* ((b-a)tgA)^2+ П* (b-a)^2tgA/CosA