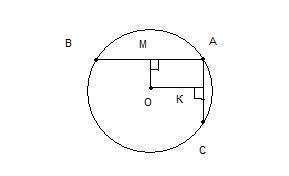
1. Расстояние от точки (в нашем случае от центра окружности) до прямой - длина перпендикуляра, проведенного из этой точки к прямой. Поэтому строим перпендикулярные отрезки ОМ и ОК, которые будут делить хорды АВ и АС пополам. ОМ=6 см, ОК=10 см по условию.
ВМ=МА=ОК=10 см,
ВА=ВМ*2=10*2=20 см
АК=КС=ОМ=6 см,
АС=АК*2=6*2=12 см
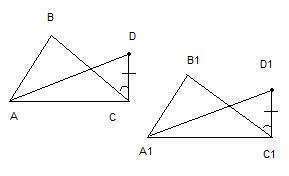
2. Треугольники ACD и A1C1D1 равны по первому признаку равенства: две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника. В нашем случае:
АС=A1C1 по условию,
CD=C1D1 по условию
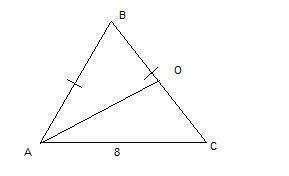
3. Pаво=АВ+ОВ+АО
Раос= АО+ОС+АС, но ОВ=ОС, т.к. АО - медиана, поэтому периметр треугольника АОС можно записать в виде:
Раос=АО+ОВ+АС
Раво-Раос=2 - по условию, поэтому запишем:
(АВ+ОВ+АО) - (АО+ОВ+АС) = 2
АВ+ОВ+АО-АО-ОВ-АС=2
АВ-АС=2
АВ=2+АС
АВ=2+8=10 см
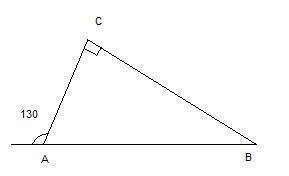
4. Зная внешний угол 130°, находим внутренний угол треугольника АВС Зная, что сумма углов треугольника равна 180°, находим