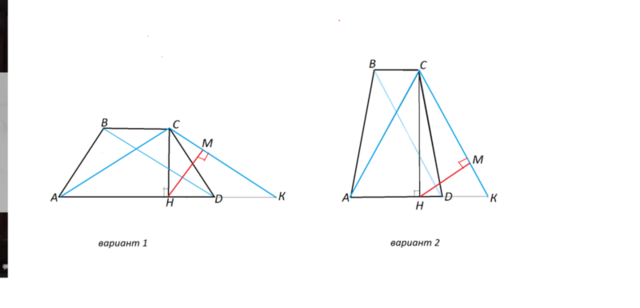
Сделаем рисунок трапеции, обозначим ее АВСD.
Проведем в ней диагонали.
Из вершины С проведем прямую СК, параллельную диагонали ВD.
Продолжим АD вправо до пересечения с СК.
Как нередко в задачах встречается, в данном решении больше рассуждений, чем вычислений.
Так как диагонали равнобедренной трапеции равны, мы получили равнобедренный треугольник АСК.
АК=АD+ВС, т.к. ВD и СК равны и параллельны, и => ВСКD - параллелограмм.
Площадь трапеции равна произведению ее высоты на полусумму оснований.
S(ABCD)=CH*(AD+BC):2
S(АСD)= СН*(АD+DК):2
DК=ВС, => S(ABCD)=S∆(АСD)
Мы доказали, что площадь треугольника АСК равна площади трапеции ABCD. Опустим из С на АК высоту СН.
СН разделила треугольник АСК на два равных прямоугольных.
Площадь каждого из них равна половине площади трапеции и равна
S ⊿CHK=12:2=6
Из Н на СК проведём высоту НМ треугольника НСК.
НМ найдем из площади ⊿НСК
S ⊿HCK=HM*CK:2
HM=2S:CK HM=12:5=2,4
Высоту трапеции мы можем найти из ⊿СНМ, а для этого надо знать длину СМ. Применим свойство высоты прямоугольного треугольника
– высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой
НМ²=СМ*МК
Пусть СМ=х, тогда МК=5-х
2,4²=СМ*(5-х)²
Отсюда получим квдратное уравнение х²-5х+5,76=0
Решив уравнение, найдем два корня - 1,8 и 3,2.
Длина высоты СН зависит от полусуммы оснований, следовательно, от их длины. Оба корня подходят.
Чтобы найти СН можно применить теорему Пифагора или свойство катета прямоугольного треугольника
– катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой
Вариант 1)
СМ=1,8, и тогда высота СН =√СМ*СК=√(1,8*5)=√9=3
вариант 2)
СМ=3,2, и тогда СН=√(3,2*5) =√16=4