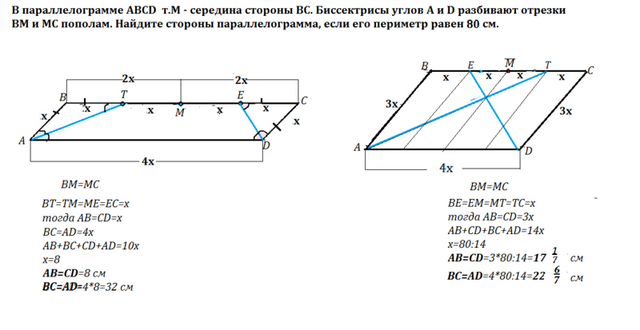
Задача имеет два решения.
1) Биссектрисы углов A и D не пересекаются;
2) Биссектрисы углов А и D - пересекаются.
Общим для обоих случаев является следующее:
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Действительно, так как биссектриса угла А параллелограмме является и секущей при параллельных ВС и АD, то ∠ ВТА=∠ ТАD как накрестлежащий. Но ∠ ТАD=∠ ТАВ по условию, следовательно, ∠ВАТ=∠АТВ.
Если в треугольнике два угла равны, то он равнобедренный.
∆ АВТ - равнобедренный. На том же основании и ∆ DEC равнобедренный.
АВ=ВТ, ЕС=СD.
Полное решение отдельно для каждого случая дано в приложении.