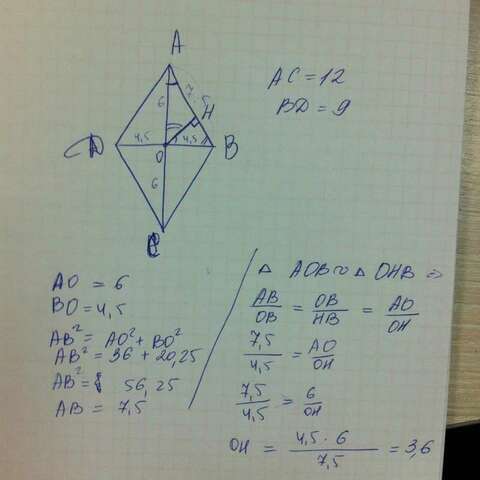
1). Расстояние от точки до прямой измеряется по перпендикуляру, значит нам нужно найти высоту треугольника AOB, проведенную из вершины прямого угла (диагонали ромба пересекаются под прямым углом).
Рассмотрим треугольник AOB, угол AOB=90 град., AB-гипотенуза, OH - высота.
Высота OH делит его на два прямоугольных треугольника.
Диагонали ромба точкой пересечения делятся пополам, значит, AO=12/2=6, OB=9/2=4,5.
AB²=AO²+OB² - по теореме Пифагора.
AB²=6²+(4,5)²
AB²=56,25
AB=7,5
2). Рассмотрим треугольники AOB и OHB, у них:
Угол HOB=90-угол B = углу A (сумма острых углов прямоугольного треугольника равна 90 градусов), углы B-совпадают, угол AOB=OHB=90 град.
Значит треугольники AOB и OHB подобны по трем углам, значит все их стороны соответственно пропорциональны:
AB/OB=AO/OH, подставляем,
(7,5)/(4,5)=6/OH
OH=(4,5)*6/(7,5)
OH=3,6
Ответ:
расстояние от точки пересечения диагоналей ромба до боковой стороны равно 3,6.