Дано:
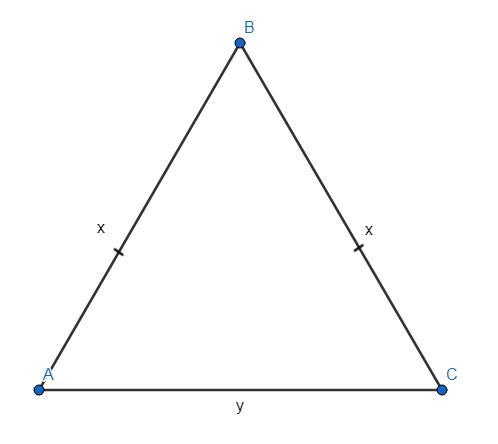
ΔАВС - равнобедренный (АВ и ВС - боковые стороны).
Р(ΔАВС) = 25 см.
Разность двух сторон = 4 см.
Найти:
АВ = ?
ВС = ?
АС = ?
Решение:
1) Итак, разность боковых сторон АВ и ВС не может быть равна 4 см, так как они равны, и при вычитании должны давать 0.
Тогда, только остаётся, что разность основания АС и боковой стороны АВ = 4 см.
Пусть боковые стороны АВ и ВС = х, а основание АС = у.
Составим систему -

АВ = ВС = х = 7 см.
АС = у = 11 см.
2) Но стоп, вдруг боковая сторона больше основания, тогда получится, что разность боковой стороны АВ и основания АС = 4 см!
Составим новую систему -


АВ = ВС = х = 29/3 см.
АС = у =  см.
см.
Ответ: 7 см, 7 см, 11 см или 29/3 см, 29/3 см, 5+(2/3) см.