Ответ:
Объяснение:
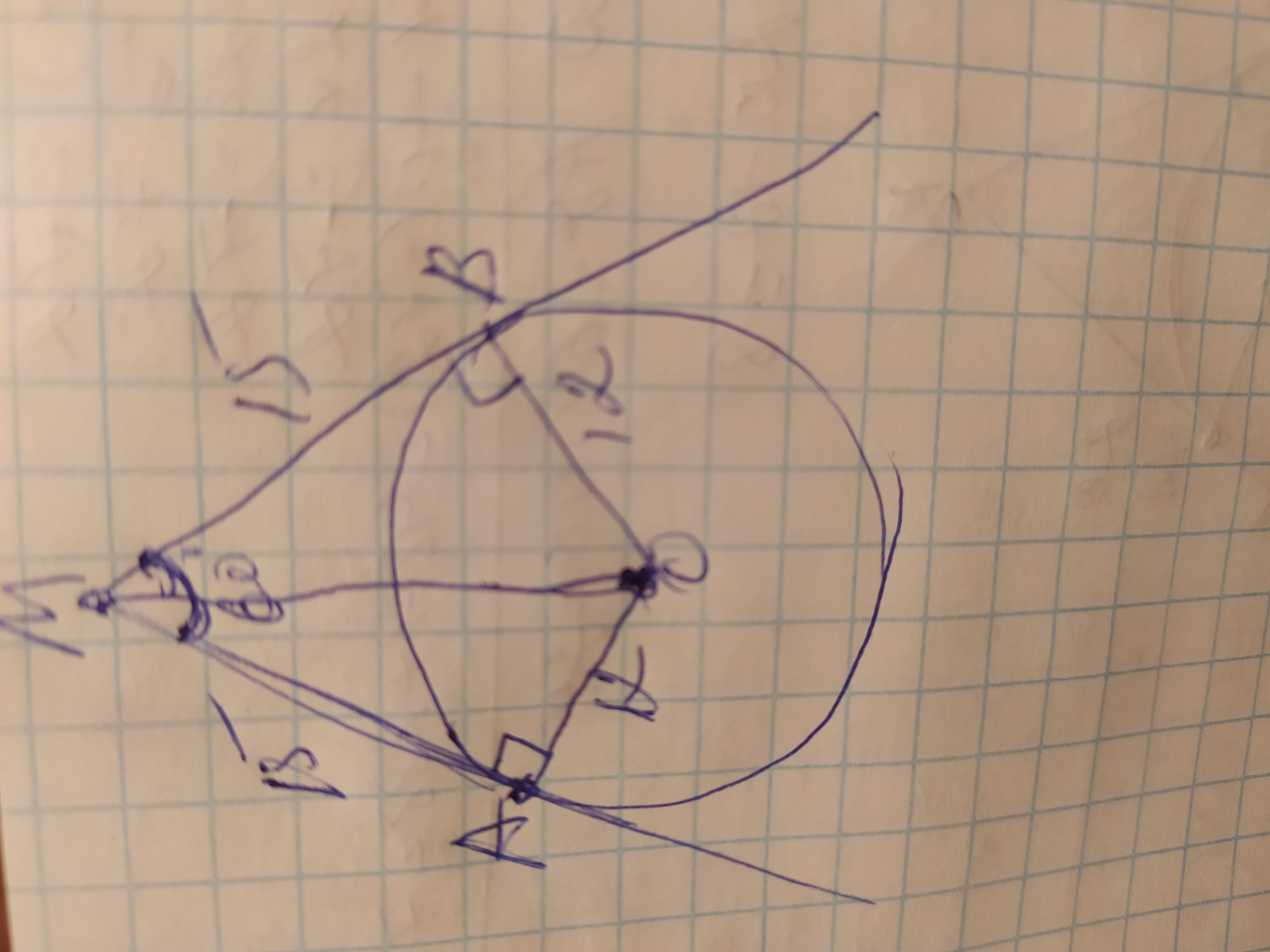
Касательные МВ =МА =15см, поскольку они пересекаются в одной точке М. Проведём отрезок ОМ, который образует два равных прямоугольных треугольника
АМО и ВСО. У них МВ=МА; ОМ=ОА=15см, по условиям, ОМ - общая сторона. Так как касательные равны между собой, то ОМ является биссектрисой и делит угол М пополам, поэтому угол АМО=углу ВСО=60÷2=30°. Радиусы, проведённые к точкам касания, образуют с ними прямоу угол =90°, следовательно ∆АМО и ∆ВМО- прямоугольные, где касательная и радиус - катеты, а ОМ- гипотенуза. Мы нашли, что один из его острых углов составляет 30°, а катет, лежащий напротив него равен половине гипотенузы. Поэтому катет ОА= ½ ОМ, значит гипотенуза ОМ будет в 2 раза больше: ОМ=12×2=24см
Итак: ОМ=24см; ОА=ОВ=12см; МА=МВ=15см