Знайти висоту ромба якщо його діагоналі 8 см і 6 см Терміново!! 40 балів

Question

Дан 1 ответ

Правильный ответ

Ответ:

Висота ромба дорівнює 4,8 см

Объяснение:

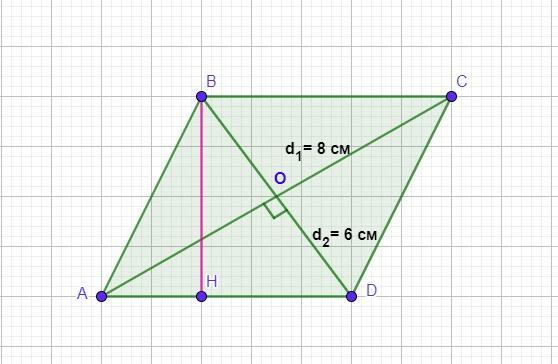
Діагоналі ромба: d₁=8 см і d₂=6 см. Знайти висоту ромба.

Ромб - це чотирикутник, у якого всі сторони рівні та протилежні сторони паралельні.

Властивості ромба:

Розглянемо ромб ABCD, діагональ АС=8 см, ВD=6 см.

Опустимо висоту ВН на бік АD (ВН⊥АD), оскількі всі висоти, опущені із будь-якого кута, рівні між собою, достатньо знайти висоту ВН.

Розглянемо прямокутний трикутник АОD(∠О=90°, так як АС⊥ВD - за властивістю).

АО=ОС=АС/2=8/2=4см

DО=ОВ=ВD/2=6/2=3см

За теоремою Піфагора знайдемо гіпотенузу АD:

АD²=АО²+DО²=4²+3²=16+9=25

АD=√25=5см

Площа ромба рівна половині добутку діагоналей:

$\boxed {\bf S=\dfrac{1}{2}d_1d_2 }$

Тоді знайдемо площу ромбу ABCD:

$\sf S_{ABCD}=\dfrac{1}{2} AC\cdot BD=\dfrac{1}{2}\cdot 8\cdot 6=24$ см²

З іншого боку площу ромба можна знайти за формулою:

$\boxed{\bf S=a\cdot h}$

а - сторона ромба

h - висота ромба

Знаходимо висоту ВН ромба ABCD:

$\sf BH=\dfrac{S_{ABCD}}{AD} =\dfrac{24}{5} =4,8$ cм

#SPJ5

ReMiDa_zn (1.2k баллов) 11 Фев, 24