Ответ: 225см²
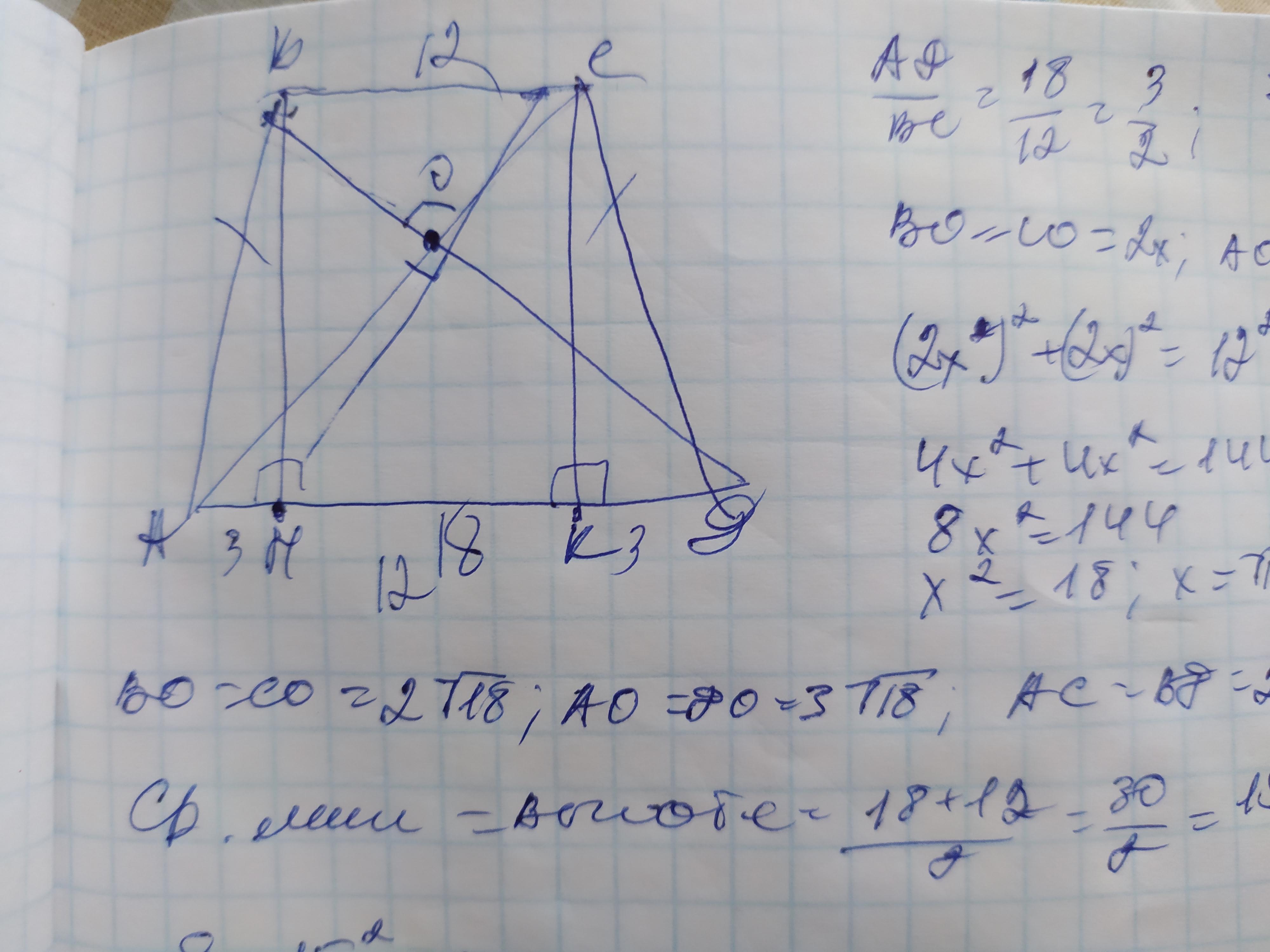
Объяснение: обозначим вершины трапеции А В С Д с основаниями ВС и АД и диагоналями АС и ВД, точку их пересечения О. Также проведём высоту ВН к нижнему основанию АД. Если диагонали равнобедренной трапеции пересекаются по прямым углом, то средняя линия трапеции равна её высоте. Средняя линия трапеции это полусумма её оснований: (АД+ВС)/2=
=(18+12)/2=30/2=15см.
Площадь трапеции вычисляется по формуле: S=ср.лин×ВН=15×15=225см²