Помогите пожалуйста буду блогадарен.

Question

Дан 1 ответ

aastap7775_zn · Answer 1 · 2024-01-24T13:43:30+0000

Сразу найдем радиус окружности. В условии сказано, что круг, ограниченный ею, и прямоугольник равновелики. Приравняв площади, найдем R - радиус окружности:

R^2 = \frac{ab}{\pi} = \frac{5*4}{\pi} = \frac{20}{\pi} => R = \sqrt{\frac{20}{\pi}} > 2.5" alt="\pi R^2 = a*b => R^2 = \frac{ab}{\pi} = \frac{5*4}{\pi} = \frac{20}{\pi} => R = \sqrt{\frac{20}{\pi}} > 2.5" align="absmiddle" class="latex-formula">

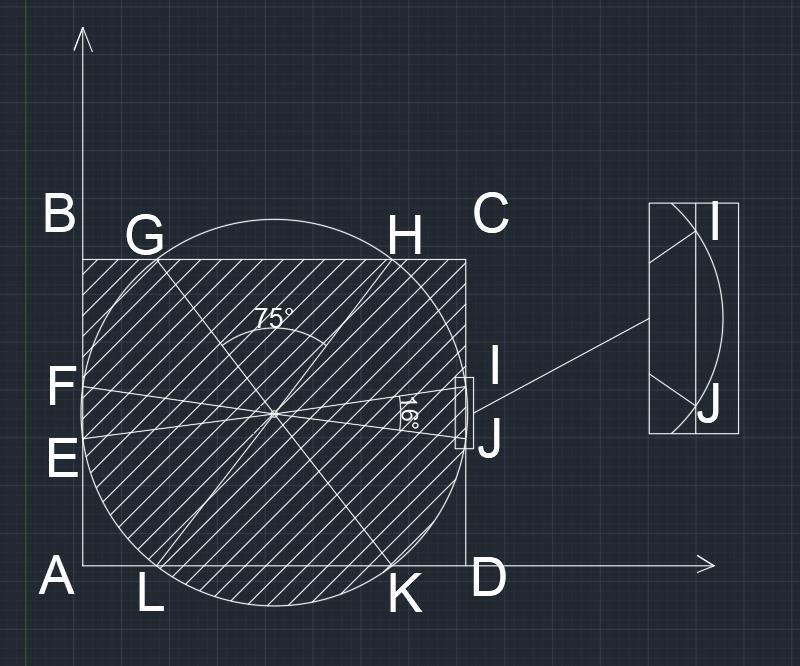
Так как радиус вышел больше 2.5, то исходный рисунок некорректен, и я прошу обратить внимание на мою схему.

С помощью Автокада находим центральные углы: тут они равны 75° и 16°.

Теперь можем найти площади сегментов, которые находятся вне прямоугольника. По формуле площади сегмента:

$S_{ceg} = \frac{R^2}{2}(\pi*\frac{\alpha^{\circ} }{180^{\circ}} - sin\alpha^{\circ} })$ , где R - это радиус окружности, а α - это угол в градусах.

Найдем площадь сегмента, который стягивается хордой GH:

$S_{cegGH} = \frac{\frac{20}{\pi}}{2}(\pi*\frac{75^{\circ} }{180^{\circ}} - sin75^{\circ}}) = \frac{10}{\pi}( \frac{5\pi}{12} - \frac{1+\sqrt{3}}{2\sqrt{2}})$

На самом деле, точно такая же площадь и у сегмента, который стягивается хордой LK из соображений симметрии.

Таким же образом находим площадь сегментов, которые стягиваются хордами EF и IJ. Они также будут равны между собой:

$S_{cegIJ} = S_{cegEF} = \frac{\frac{20}{\pi}}{2}(\pi*\frac{16^{\circ} }{180^{\circ}} - sin16^{\circ}}) = \frac{10}{\pi}( \frac{4\pi}{45} - sin\frac{4\pi}{45})$ .

К сожалению, синус нельзя представить в виде выражения, поэтому так и оставим.

Осталось найти площадь криволинейной трапеции AEL. В силу соображений симметрии, три таких же трапеции будут иметь такую же площадь.

Найдем координату точки L из следующих соображений:

Точка L лежим на прямой y = 0.

Уравнение окружности имеет вид:

$(x-x_0)^2+(y-y_0)^2 = R^2$ , где $x_0, y_0, R$ - это координаты центра окружности и ее радиус соответственно. В нашем случае

$x_0 = 2.5, y_0 = 2, R = \sqrt{\frac{20}{\pi}}$

Для того, чтобы найти точку пересечения, подставим y = 0 в уравнение, и найдем x:

$(x-2.5)^2+(y-2)^2 = \frac{20}{\pi} \\(x-2.5)^2+(0-2)^2 = \frac{20}{\pi} \\(x-2.5)^2 + 4 = \frac{20}{\pi}\\(x-2.5)^2 = \frac{20}{\pi} - 4\\x-2.5 = \pm\sqrt{\frac{20}{\pi} - 4}\\x = 2.5 \pm\sqrt{\frac{20}{\pi} - 4}$

Возьмем знак минус, так как со знаком плюс будет точка K. Итого: координата точки $L(\frac{5}{2} - \sqrt{\frac{20}{\pi} -4}};0) \approx L(0.9618;0)$

Теперь найдем координату точки E. Тут почти все тоже самое, только она лежит на прямой x = 0. Подставим в уравнение окружности и найдем y:

$(x-2.5)^2+(y-2)^2 = \frac{20}{\pi} \\(0-2.5)^2+(y-2)^2 = \frac{20}{\pi} \\6.25 + (y-2)^2 = \frac{20}{\pi}\\(y-2)^2 = \frac{20}{\pi} - 6.25\\y-2 = \pm\sqrt{\frac{20}{\pi} - 6.25}\\y = 2 \pm\sqrt{\frac{20}{\pi} - 6.25}$

Также возьмем с минусом, так как с плюсом будет точка F.

Таким образом, координата точки E имеет вид:

$E(2-\sqrt{\frac{20}{\pi}-6.25 } ;0) \approx E(1.65...;0)$

PS: остальное завтра допишу.