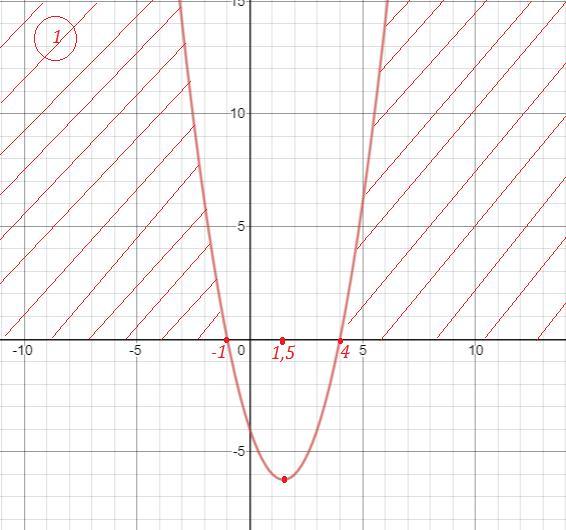
парабола, точки пересечения с ОХ - (-1,0) и (4,0), вершина в точке (1,5 ; -6,25) . Рис. 1 .
парабола, точки пересечения с ОХ - (-1,0) и (4,0), вершина в точке (1,5 ; -6,25) . Рис. 1 .
![x\in (-\infty ;-1\, ]\cup [\, 4\, ;\, +\infty ) x\in (-\infty ;-1\, ]\cup [\, 4\, ;\, +\infty )](https://tex.z-dn.net/?f=x%5Cin%20%28-%5Cinfty%20%3B-1%5C%2C%20%5D%5Ccup%20%5B%5C%2C%204%5C%2C%20%3B%5C%2C%20%2B%5Cinfty%20%29)

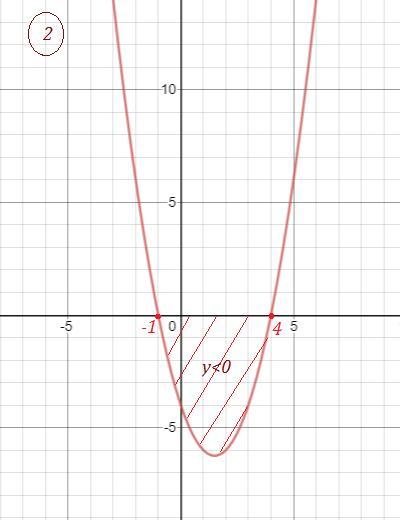
Та же парабола. Рис. 2 . ![x\in [-1\, ;\, 4\; ]\; . x\in [-1\, ;\, 4\; ]\; .](https://tex.z-dn.net/?f=x%5Cin%20%5B-1%5C%2C%20%3B%5C%2C%204%5C%3B%20%5D%5C%3B%20.)

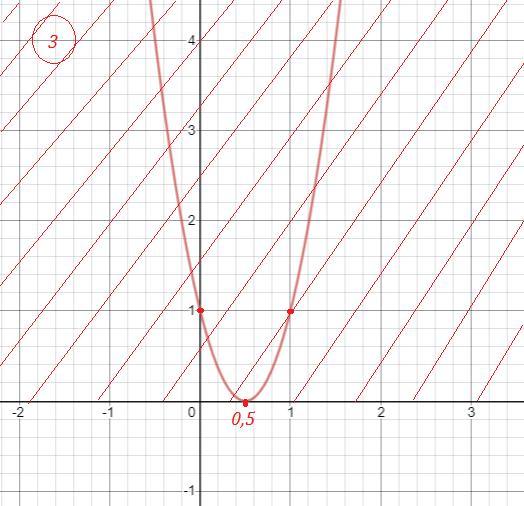
Парабола касается оси ОХ в вершине, точке (1/2 ; 0) . Неравенство выполняется при всех действительных значениях переменной 
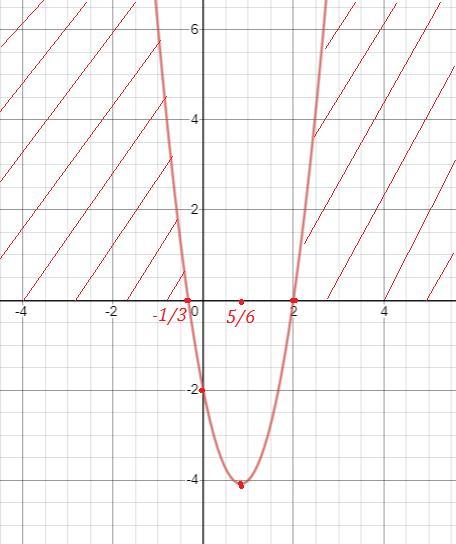
 0\\\\3x^2-5x-2=0\; \; ,\; \; D=49\; \; ,\; \; x_1=-\frac{1}{3}\; ,\; \; x_2=2" alt="4)\; \; 3x^2-5x-2>0\\\\3x^2-5x-2=0\; \; ,\; \; D=49\; \; ,\; \; x_1=-\frac{1}{3}\; ,\; \; x_2=2" align="absmiddle" class="latex-formula">
0\\\\3x^2-5x-2=0\; \; ,\; \; D=49\; \; ,\; \; x_1=-\frac{1}{3}\; ,\; \; x_2=2" alt="4)\; \; 3x^2-5x-2>0\\\\3x^2-5x-2=0\; \; ,\; \; D=49\; \; ,\; \; x_1=-\frac{1}{3}\; ,\; \; x_2=2" align="absmiddle" class="latex-formula">
Парабола проходит через точки (-1/3;0) , (2;0) , (0,-2) .