Найти площадь фигуры, ограниченной параболой у = + 3х и осью Ох;

Ответ:

S=4,5 квадратных единиц

Пошаговое объяснение:

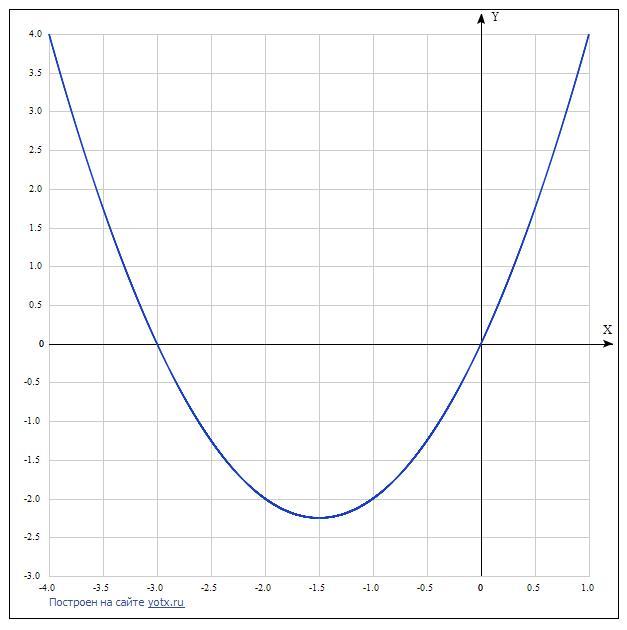
Надо найти пересечение параболы с осью ОХ.

х²+3х=0

х(х+3)=0

х₁=0, х₂=-3.

Значит пределы интегрирования будут от (-3) до 0.

$\int\limits^{0}_{-3} {(x^2+3x)} \, dx=\left(\frac{x^3}{3}+\frac{3x^2}{2}\right)|_{-3}^0=\left(\frac{0^3}{3}+\frac{3*0^2}{2}\right)-\left(\frac{(-3)^3}{3}+\frac{3*(-3)^2}{2}\right)=$

$=-\left(\frac{(-27)}{3}+\frac{3*3^2}{2}\right)=-\left(-9+\frac{27}{2}\right)=9-\frac{27}{2}=9-13,5=-4,5$

Так как эта часть параболы находится ниже оси ОХ, то интеграл получился отрицательным. А площадь равна модулю от этого интеграла, то есть S=4,5 квадратных единиц.

График функции прикрепляю.