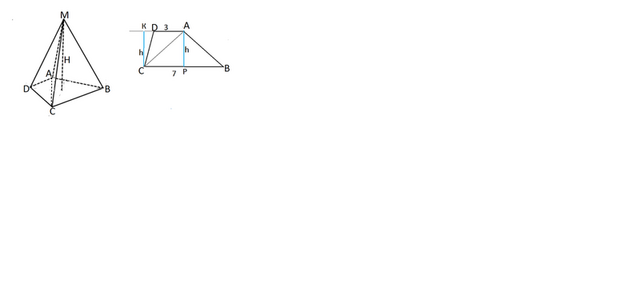
В основании пирамиды MABCD лежит трапеция ABCD с основаниями ВС = 3 см и AD = 7 см. Объем пирамиды МАВС на 4 м3 (в кубе) больше объема пирамиды MACD. Найдите объем пирамиды MABCD.
Думаю, что условие дано с опечаткой, и разница 4м³ должна означать 4см³
А большее основание не АД, а ВС, иначе объем пирамиды МАВС не может быть больше объема пирамиды МАВД (при равных высотах больше объем той пирамиды, площадь основания которой больше).
----------------
Решение дается по скорректированному условию:
В основании пирамиды MABCD лежит трапеция ABCD
с основаниями ВС = 7 см и AD = 3 см.
Объем пирамиды МАВС на 4 см³ больше объема пирамиды MACD. Найдите объем пирамиды MABCD. ( В случае необходимости можно самостоятельно пересчитать по данному способу решения)
------------------
Сделав рисунок, легко заметить, что эти две пирамиды - части исходной и имеют одну и ту же высоту Н ( т.е. высоту пирамиды МАВСD).
(Надеюсь, на этот раз рисунок загрузится - несколько раз не грузился)
Треугольники в основании этих пирамид имеют высоты СК и АР, равные высоте h трапеции АВСD.
Сделаем и рисунок основания - трапеции ABCD.
В ней треугольник АВС - остроугольный, высота АР расположена внутри него.
Треугольник АDС тупоугольный, высота СК из С идет к продолжению АD).
Объём пирамиды МАВС равен 1/3 произведения площади основания на высоту, т.е. площади треугольника АВС на высоту Н пирамиды MABCD
S ABC=0,5h·7
V(MABC)=0,5h·7·H:3
Объём пирамиды МАDС равен 1/3 произведения площади основания на высоту, т.е. площади треугольника АDС на высоту H пирамиды MABCD.
S ADC=0,5h·3
V(MADC)=0,5h·3·H:3
По условию
V(MABC) - V(MADC)=4 см³
0,5h·7·H:3-0,5h·3·H:3 =4 см³
Домножим обе части уравнения на 6
h·7·H - h·3·H=24 см³
h·4·H=24 см³ ( длина h, H и 4 выражена в см, поэтому результат умножения - см³)
Делим 24 см³ на 4см - разницу длин оснований трапеции ( или оснований треугольников, ее составляющих - разница оснований одна и та же) и получим
hH=24:4=6 см²
Объем пирамиды MABCD равен 1/3 произведения площади основания на её высоту. Площадь основания пирамиды равна площади трапеции ABCD
S (АВСD)=h(ВС+АД):2=h·5
Подставим это значение в формулу объёма пирамиды:
V=SH:3
V=5h·H:3
Но мы вычислили, что hH=6 см²
V=5h·H=5см·6см²:3=10 см³