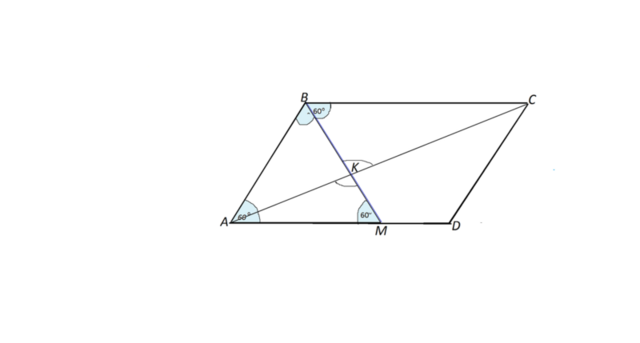
ВМ-биссектриса угла В.
Биссектриса параллелограмма отсекает равнобедренный треугольник, в данном случае треугольник ВАМ.
Так как угол А=60°, а сумма углов при одной стороне параллелограмма равна 180° , угол В=180°-60°=120°, и углы, на которые делит его биссектриса, равны каждый по 60°.
Следовательно, треугольник АВМ - равносторонний, и ВМ=АВ=АМ=10 см
Рассмотрим треугольник АВС.
АВ=10 см
ВС=АD=10+5=15 см
Биссектриса треугольника делит противолежащую углу сторону на отрезки, пропорциональные прилежащим сторонам.
Следовательно, АК:КС=АВ:ВС=10:15 и равно 2:3.
Рассмотрим треугольники АМК и ВСК.
Они имеют по два равных угла. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
АМ:ВС=АК:КС=КМ:ВК
Так как отношение АК:КС=2:3, то КМ:ВК=2:3
ВМ=10, и отсюда
ВК=3/5 ВМ=6 см,
КМ=2/5 ВМ=4 см