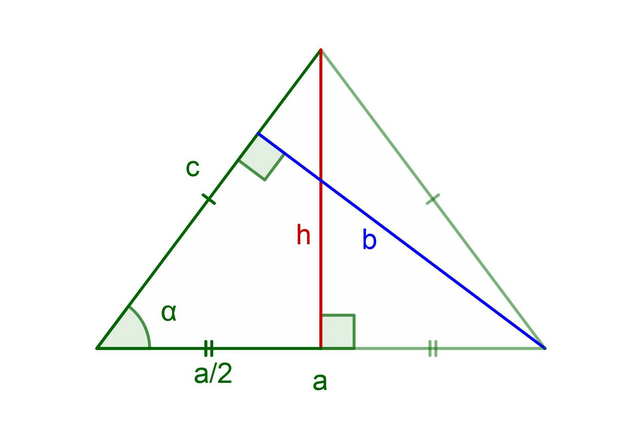
Дано: Кут α при основі рівнобедреного т-ка; висота b, опущена на бічну сторону. Знайти бічну сторону.
Рішення:
Нехай основа рівнобедреного Δ дорівнює a.
Виразимо а через синус кута α:

Проведемо висоту h до основи a. Виразимо h через тангенс кута α:

Нехай бічна сторона т-ка рівна c. Знайдемо площу Δ:

Виразимо сторону c через площу тр-ка:

Відповідь: бічна сторона рівнобедреного т-ка рівна відношенню висоти, проведеної на бічну сторону, на синус подвійного кута α.