Основание AB треугольника ABC равно 26 см медианы AK и BM проведенные к боковым сторонам...

Ответ:

$S_{\Delta ABC} = 720 ~(cm^{2})$

Объяснение:

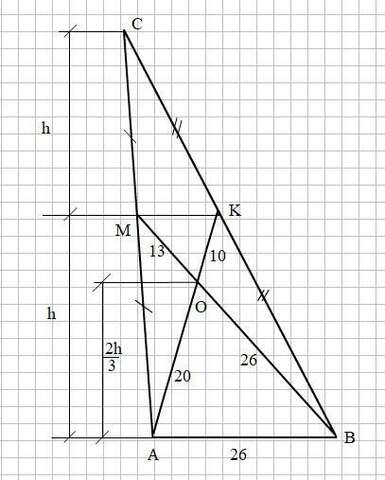
Смотри прикреплённый рисунок

Медианы АК и ВМ точкой пересечения О делятся в отношении 2:1, начиная от вершины, поэтому АО = 2/3 · 30 = 20 (см), ОК = 1/3 · 30 = 10(см), ВО = 2/3 · 39 = 26 (см), ОМ = 1/3 · 39 = 13 (см).

Периметр ΔАОВ равен Р = АВ + АО + ВО = 26 + 20 + 26 = 72 (см). Полупериметр ΔАОВ равен р = 72 : 2 = 36 (см)

Площадь ΔАОВ

$S_{\Delta AOB} =\sqrt{p(p-AB)(p - AO)(P-BO)} =$

$=\sqrt{36(36 - 26)(36-20)(36-26)} = 240 ~(cm^2)$

Площадь ΔАОВ также равна

$S_{\Delta AOB} = 0.5\cdot AB\cdot \frac{2}{3}h = 0.5 \cdot 26 \cdot \frac{2}{3}h= 240$

h = 240 · 3 : 26 = 360/13 (см)

Высота ΔАВС равна 2h

Площадь ΔАВС

$S_{\Delta ABC} = 0.5 \cdot AB\cdot 2h = AB\cdot h = 26 \cdot \dfrac{360}{13} = 720 ~(cm^{2})$