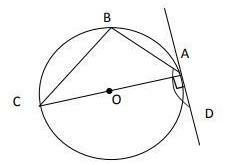
OA - радиус, причём проведённый в точку касания, поэтому ∠СAD = 90°. ⇒ ∠BAC = ∠BAD-∠CAD = 120°-90° = 30°.
Рассмотрим ΔАВС. Так как АС - диаметр, тогда дуга АС - полуокружность. ∠АВС опирается на полуокружность, значит, ∠АВС = 90°.
Следовательно, если ΔАВС - прямоугольный, тогда ∠ВСА = 90°-∠BAC = 90°-30° = 60°.
Ответ: 60°.