Ответ:
28√2 см
Объяснение:
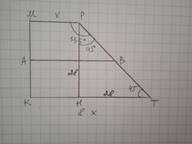
Дано: КМРТ - трапеция, КМ⊥КТ, ∠МРТ=135°, АВ - средняя линия, АВ=18 см. Найти РТ.
Проведем высоту РН. Рассмотрим ΔНРТ - прямоугольный.
∠НРТ=135°-90°=45°, значит и ∠Т=45°, т.к. сумма острых углов прямоугольного треугольника составляет 90°.
ΔНРТ - равнобедренный и НР=НТ.
Пусть МР=х см, тогда КТ=8х см. Средняя линия трапеции равна полусумме оснований, значит
АВ=(х+8х)/2; 9х/2=18; 9х=36; х=4
МР=4 см, КТ=8*4=32 см.
НК=МР; НТ=32-4=28 см.
НР=НТ=28 см
По теореме Пифагора
РТ²=НР²+НТ²=784+784=1568
РТ=√1568=28√2 см