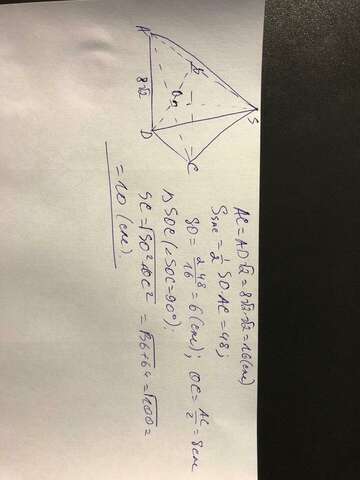
Ответ:
Чертеж и весь счет во вложении.
Заметим, что в правильной четырехугольной пирамиде основание высоты совпадает с точкой пересечения диагоналей основания (точка О на рисунке). Следовательно, отрезок SO перпендикулярен плоскости ABC. Так как прямая AC лежит в плоскости ABC, то SO⊥AC (угол SOC прямой). Тогда SC можно найти из теоремы Пифагора для прямоугольного треугольника SOC. Нам понадобятся длины катетов SO и OC.
AC - диагональ квадрата ABCD. Значит, AC = AD*√2. OC = AC/2.
Диагональным сечением, очевидно, является треугольник SAC. Его площадь известна из условия. Зная ее и AC, находим SO.
Дальше вычисляем SC.
Ответ: 10 см