Решение:
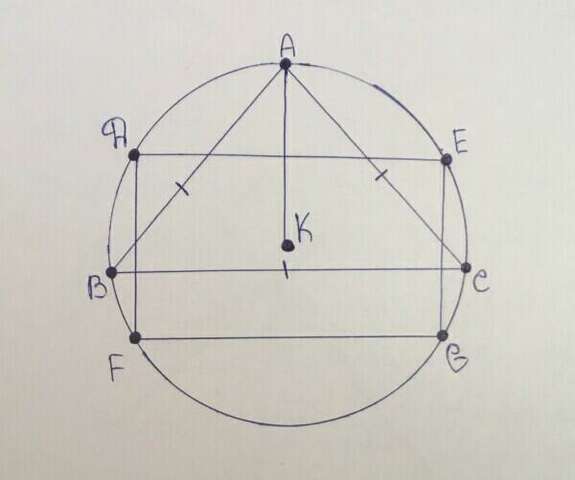
Пусть дана окружность с центром в точке K, равносторонний треугольник ABC и вписанный квадрат DEFG.
Периметр треугольника это сумма всех длин его сторон.
Т.к. треугольник ABC - равносторонний, то AB=BC=AC=18/3=6 (см).
Проведём из точки B равностороннего треугольника АВС отрезок к центру окружности в точке К так, что отрезок АК - радиус данной окружности.
Вспомним формулу радиуса равностороннего треугольника: R=a:√3.
=> радиус равностороннего треугольника АВС=6:√3=(6√3)/3=2√3 (см).
Вспомним формулу стороны описанного квадрата: a=R√2.
=> сторона вписанного квадрата DEFG=2√3*√2=2√(3*2)=2√6 (см).
В квадрате все стороны между собой равны.
=> DE=EG=GF=FD=2√6 (см).
Ответ: сторона DE вписанного квадрата DEFG равна 2√6 (см).