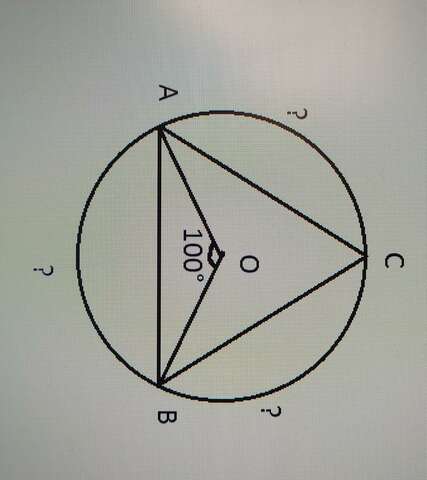
(чертёж прикреплён)
- - - - - - - - - - - - - - - - - - -
*решение*:
Если О - центр окружности, то угол АОВ - центральный.
Центральный угол равен дуге, на которую опирается. Отсюда, дуга АВ = 100°.
Угол САВ = углу СВА, тогда дуга АС = дуге ВС = (360° - 100°) / 2 = 260° / 2 = 130°.
Ответ: АВ = 100°, АС = ВС = 130°.