УМОЛЯЮ ПОМОГИТЕ ОЧЕНЬ НУЖНО ПОЖАЛУЙСТА УМОЛЯЮ

$\displaystyle y=\frac{6+36x}{6x^2+x} =\frac{6(1+6x)}{x(6x+1)}\\\\\left \{ {{y=\dfrac6x\;} \atop {x\ne-\dfrac16}} \right.$

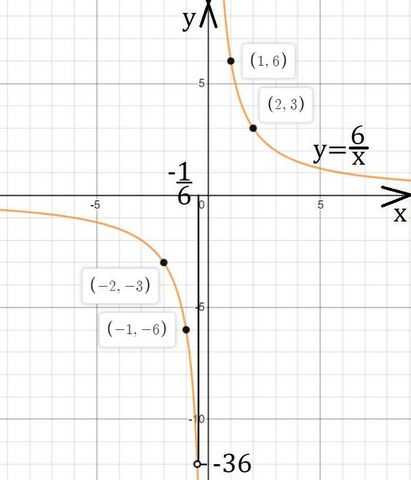
y = 6/x - функция обратной пропорциональности (y=a/x), графиком будет гипербола в 1 и 3 четверти т.к. a=6>0.

При x=-1/6: y=-36

При x=1: y=6

При x=-1: y=-6

При x=-2: y=-3

При x=2: y=3

По этим точкам построим график.

Прямая прямой пропорциональности y=kx будет иметь одну общею точку, когда она пройдёт через выколотую точку (-1/6;-36)

-36 = k·(-1/6) ⇔ k=36·6=216

Ответ: 216.

УМОЛЯЮ ПОМОГИТЕ ОЧЕНЬ НУЖНО ПОЖАЛУЙСТА УМОЛЯЮ​