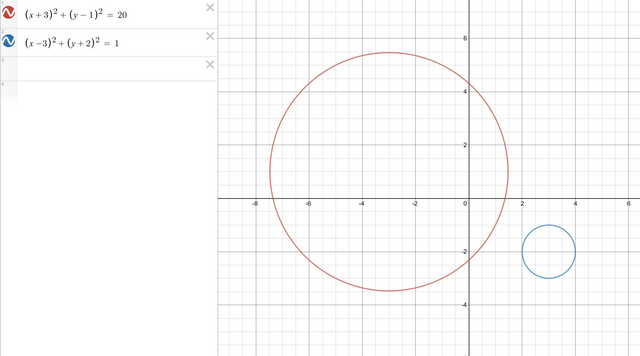
Ответ:
Круги не пересекаются.
Пошаговое объяснение:
Центр 1-го круга в т. (-3;1), центра второго круга в т. (3; -2)
По т. Пифагора найдём расстояние между центрами
L = √(Δx² + Δy²) = √(6² + 3²) = √(36 + 9) = √45 = √9*5 = 3√5
Сумма радиусов S = √20 + √1 = √4*5 + 1 = 2√5 + 1
Поскольку √5 > 1, то
3√5 > 2√5 + 1
Т.е. расстояния между центрами больше суммы радиусов. Значит окружности не пересекаются. Данный ответ легко проверить построив графики окружностей. См. рисунок