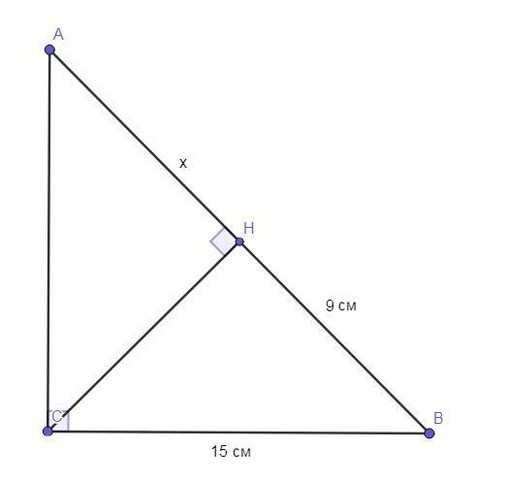
Чертёж смотрите во вложении.
Дано:
ΔABC - прямоугольный.
∠С = 90°.
СН - высота, проведённая к гипотенузе АВ.
НВ - проекция катета СВ на гипотенузу АВ = 9 см.
СВ = 15 см.
Найти:
S(ΔАВС) = ?
P(ΔАВС) = ?
Решение:
Пусть АН = х.
По свойству проекций -

АB = 9 (cм)+х.
Подставим в формулу известные нам значения и решим полученное уравнение -

АН = х = 16 см.
АВ = 9 см+16 см = 25 см.
По теореме Пифагора -

Подставим в формулу известные нам значения и найдём значение АС -

AC = 20 см.
P(ΔАВС) = АС+АВ+СВ = 20 см+25 см+15 см = 60 см.
Площадь прямоугольного треугольника равна половине произведения его катетов -
S(ΔABC) = 0,5*CB*AC
S(ΔABC) = 0,5*15 см*20 см
S(ΔABC) = 150 см².
Ответ: 150 см², 60 см.