В равнобедренном треугольнике точка касания вписанной окружности делит боковую сторону **...

Question

В равнобедренном треугольнике точка касания вписанной окружности делит боковую сторону на отрезки длиной 12 см и 3 см, считая от основания. Найдите площадь треугольника.

Comments

9x12=...

Answer 1

Ответ:

108 см²

Пошаговое объяснение:

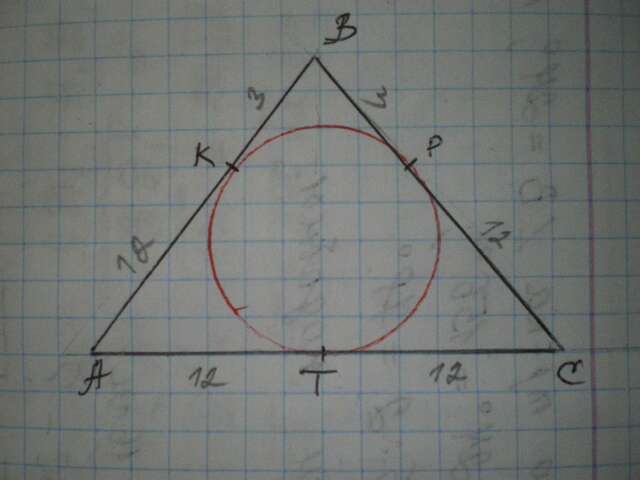
Дан ΔАВС, АВ=ВС, РС=АК=12 см,  КВ=ВР=3 см. Найти S(АВС)

ТС=РС=12 см,  АТ=АК=12 см как касательные к окружности, проведенные из одной точки

АС=12+12=24 см

АВ=ВС=12+3=15 см

Найдем площадь по формуле Герона:

S=√(p(p-a)(p-b)(p-c)=√(27*3*12*12)=√11664=108 см²

---

Comments

А заметить, что у тр-ка BTC гипотенуза 15 и один катет 12, то есть это египетский тр-к (9,12,15), и площадь двух таких тр-ков 9*12*2/2 = 108 ....?