Ответ:
S = 
Пошаговое объяснение:
площадь полной поверхности цилиндра
S = 2πr2 + 2πrh где r - радиус основания цилиндра, h - высота цилиндра
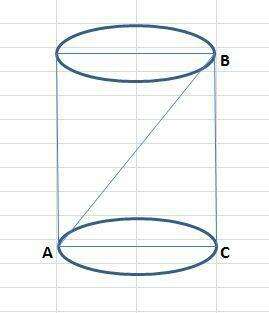
высоту ищем из ΔАВС катет, лежащий напротив угла в 30° равен половине гипотенузы. у нас получается h = 1.5
теперь по теореме Пифагора считаем второй катет (или диаметр круга) АС = 
отсюда r = 
теперь посчитаем S =