Ответ:
700/28*5=125
Объяснение:
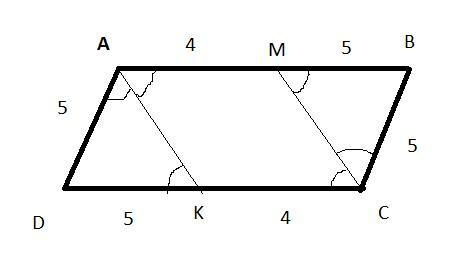
Обозначим параллелограмм ABCD так, что углы A и C - тупые. Проведем биссектрисы AK, и CM. Т.к. ABCD - параллелограмм, то углы DAB и BCD равны, и соответственно т.к. AK и CM биссектрисы, то углы
углы
углы
в итоге
Вводим условные единицы длины, с учетом того, что биссекутрисса делит противоположную сторону в соотношениие 4:5 так, что BM=5уе, AM=4уе, далее очевидно периметр параллелограмма равен 28 уе, 1уе=700/28=25
Очевидно из рисунка - меньшая сторона параллелограмма равна 5уе=5*25=125