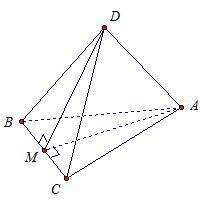
Ответ:
Объяснение:
пусть М - середина отрезка BC. треугольник ABC– равнобедренный, так как АВ = АС. Тогда медиана АМ является и высотой, то есть AM перпендикулярна BC
Треугольник DВС – равнобедренный, так как DВ = DС. Тогда медиана DМ является и высотой, то есть DM перпендикулярна BC
Прямая ВС перпендикулярна двум пересекающимся прямым DM и AM из плоскости DMA, а значит, прямая ВС перпендикулярна прямой DA, которая лежит в плоскости DMA, что и требовалось доказать.