Ответ: a) x∈(-3;-1)U(1;3)U(5;+∞)
; б) x∈(-∞;-3)U(-1;1)U(3;5); в) x₁ = -1, х₂ = 3;
г) x₁ = -3, х₂ = 1, х₃ = 5
Пошаговое объяснение:
Функцiя y = f(x) визначена на всiй множинi дiйсных чисел.
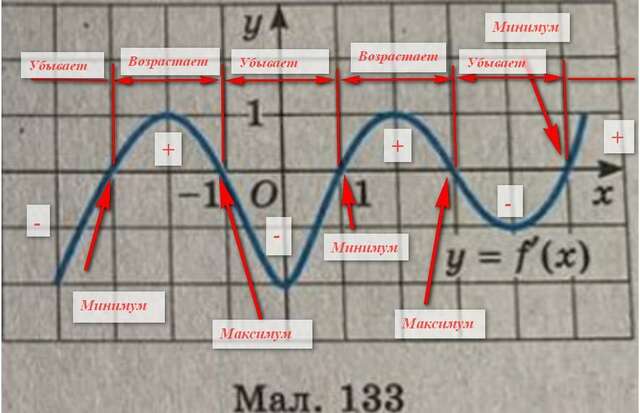
На малюнку 133 зображено графiк функцii y=f'(x).
Користуючись зображениям, укажить:
a) промежки на яких функцiя y=f(x) зростає
б) промежки на яких функцiя y=f(x) спадає
в) точки максимуму функцiї y=f(x)
г) точки мінiмума функції y=f(x)
Функция y = f (x) определена на всем множестве действительных чисел.
На рисунке 133 изображен график функции y=f'(x).
Пользуясь изображениям, укажите:
a) промежутки на которых функция y=f(x) возрастает
б) промежутки на которых функция y=f(x) убывает
в) точки максимума функции y=f(x)
г) точки минимума функции y=f(x)
a)Функция возрастает на промежутках где производная функции больше нуля f'(x)>0
x∈(-3;-1)U(1;3)U(5;+∞)
б)Функция убывает на промежутках где производная функции меньше нуля f'(x)<0</p>
x∈(-∞;-3)U(-1;1)U(3;5)
в)Если производная меняет свой знак с "+" на "-", т.е. функция меняет возрастание на убывание в некоторой точке, то такая точка и есть точка максимума функции.
Следовательно функция имеет локальный максимум в точках
x₁ = -1 х₂ = 3
г) Если производная меняет свой знак с "-" на "+", т.е. функция меняет убывание на возрастание в некоторой точке, то такая точка и есть точка минимума функции.
Следовательно функция имеет локальный минимум в точках
x₁ = -3 х₂ = 1 х₃ = 5
a) функція зростає на проможутках де похідна функції більше нуля f'(x)>0
х∈ (-3;-1)U (1; 3) U (5; oo)
б) функція убуває на проможутках де похідна функції менше нуля f'(x)<0</p>
х∈(-oo;-3)U(-1;1)U(3; 5)
в) якщо похідна змінює свій знак з "+" на "-", тобто функція змінює зростання на спадання
в деякій точці, то така точка і є точка максимуму функції.
Отже функція має локальний максимум в точках
x₁ = -1 х₂ = 3
в) якщо похідна змінює свій знак з "-" на "+", тобто функція змінює спадання на зростання
в деякій точці, то така точка і є точка мінімуму функції.
Отже функція має локальний мінiмума в точках
x₁ = -3 х₂ = 1 х₃ = 5