Ответ:
В Δ OPN
∠O=70°
∠P=90°
∠N=20°
Объяснение:
План решения:
1. доказывем,что ΔOPN - прямоугольный (∠P=90°)
2.нахoдим угол ∠ONK
3. от ∠ONK отнимаем заданный в условии ∠PNK и получам ∠N (в Δ ONP).
4. два угла найдены, находим ∠ O=90°- ∠ N (в Δ ONP).
Решение.
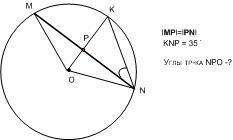
1. Определим, чему равен ∠ OPN. Для чего проведем радиус в точку M.
Рассмотрим Δ MON. Этот треугольник - равнобедренный с основанием [MN], и боковыми сторонами [OM] и [ON] (т.к.l ON l = l OM l, как радиусы окружности).
Итак в равнобедренном Δ MON на основание опущена медиана [OP] (по условию l MP l=l NP l). а у равнобедренного треугольника медиана, опущенная на основание совпадает и с бисектриссой и с высотой (свойства равнобедренных треугольников)! А раз [OP] - это и высота, то ∠ OPN = ∠ OPM = 90 ° (по определению высоты треугольника). Значит ΔONP и ΔKNP - прямоугольные!
2. Теперь рассмотрим прямоугольный Δ KNP. Его углы:
∠ KNP =35° (по условию), ∠ KPN =90°, следовательно
∠ PKN=180°-90°-35°=55°.
3. Теперь рассмотрим Δ KNO. Этот треугольник равнбедренный с боковыми сторонами [OK] = [ON] , как радиусы окружности. В этом равнобедренном треугольнике угол при основании ∠ OKN = ∠ PKN (отрезок [PO]l ∈ [OK] - т.е. это один и тот же угол). Следовательно ∠ ONK = ∠ OKN = ∠ PKN = 55° (углы при основании равнобедренного треугольника).
А ∠ ONK= ∠ KNP + ∠ ONP;
∠ ONP = ∠ ONK - ∠ KNP
∠ ONP = 55° - 35° =20°;
4. И наконец рассмотрим Δ ONP.
В нем угол ∠P =90°. ∠ONP=20°.Следовательно
∠PON = 180° - 90° - 20° = 70°. Все.