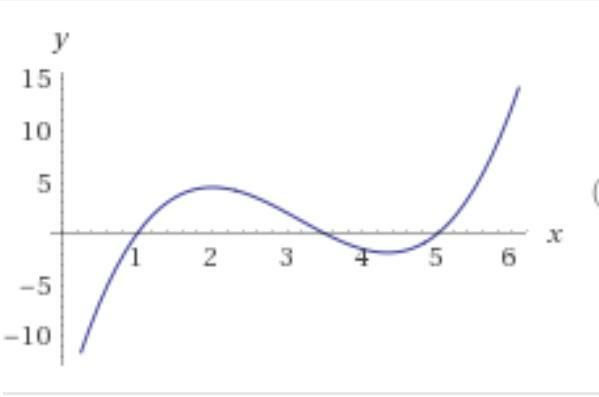
Будем считать, что надо найти корни заданного кубического выражения.
y=x^3-9,5x^2+26x-17,5 = 0.
Один корень явно виден - это х = 1.
Разделим многочлен на (х - 1):
x^3 - 9,5x^2 + 26x - 17,5 |x - 1
x^3 - x^2 x^2 - 8,5x + 17,5
-8,5x^2 + 26x
-8,5x^2 + 8,5x
-17,5x - 17,5
-17,5x - 17,5
0
Полученный квадратный трёхчлен разложим на множители, найдя его корни.
Решаем уравнение x^2 - 8,5*x + 17,5=0.
Ищем дискриминант:
D=(-8.5)^2-4*1*17.5=72.25-4*17.5=72.25-70=2.25;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(-(√2,25-8,5))/(2*1)=(1,5-(-8,5))/2=(1,5+8,5)/2=10/2=5;
x_2=(-√2,25-(-8,5))/(2*1)=(-1,5-(-8,5))/2=(-1,5+8,5)/2=7/2=3,5.
Ответ: имеем три корня х = 1, х = 3,5 и х = 5.