Продолжение продолжения - Все ответы

Дан 1 ответ

Правильный ответ

$\begin{cases} x_1'=-x_1+3x_2\\ x_2'=2x_1-x_2 \end{cases}$

Продифференцируем первое уравнение:

$x_1''=-x_1'+3x_2'$

Подставим выражение для $x_2'$ :

$x_1''=-x_1'+3(2x_1-x_2)$

$x_1''=-x_1'+6x_1-3x_2$

Сложим полученное уравнение с первым уравнением системы:

$x_1''+x_1'=-x_1'+6x_1-3x_2-x_1+3x_2$

$x_1''+2x_1'-5x_1=0$

Составим характеристическое уравнение:

$\lambda^2+2\lambda-5=0$

$D_1=1^2-1\cdot(-5)=6$

$\lambda_1=-1-\sqrt{6};\ \lambda_2=-1+\sqrt{6}$

$x_1=C_1e^{(-1-\sqrt{6}) t}+C_2e^{(-1+\sqrt{6}) t}$

Найдем первую производную:

$x_1'=(-1-\sqrt{6})C_1e^{(-1-\sqrt{6}) t}+ (-1+\sqrt{6})C_2e^{(-1+\sqrt{6}) t}$

Выразим из первого уравнения $x_2$ :

$x_2=\dfrac{x_1'+x_1}{3}$

$x_2=\dfrac{(-1-\sqrt{6})C_1e^{(-1-\sqrt{6}) t}+(-1 +\sqrt{6})C_2e^{(-1+\sqrt{6}) t} +C_1e^{(-1-\sqrt{6}) t}+C_2e^{(-1+\sqrt{6}) t} }{3}$

$x_2=-\dfrac{\sqrt{6}}{3}C_1e^{(-1-\sqrt{6}) t}+\dfrac{\sqrt{6}}{3}C_2e^{(-1+\sqrt{6}) t}$

Общее решение:

$\begin{cases} x_1=C_1e^{(-1-\sqrt{6}) t}+C_2e^{(-1+\sqrt{6}) t} \\ x_2=-\dfrac{\sqrt{6}}{3}C_1e^{(-1-\sqrt{6}) t}+\dfrac{\sqrt{6}}{3}C_2e^{(-1+\sqrt{6}) t}\end{cases}$

Для определения точек равновесия составим характеристическое уравнение с коэффициентами из правых частей уравнений:

$k^2-(a_{11}+a_{22})k+a_{11}a_{22}-a_{12}a_{21}=0$

$k^2-(-1-1)k+(-1)\cdot(-1)-3\cdot2=0$

$k^2+2k-5=0$

$k=-1\pm\sqrt{6}$

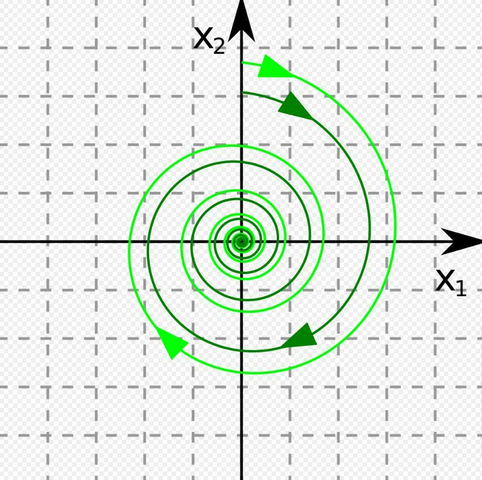
Так как получившиеся числа комплексные с ненулевой действительной частью, то тип точки равновесия - фокус (устойчивый фокус, так как действительная часть отрицательна).

Artem112_zn (271k баллов) 15 Март, 21