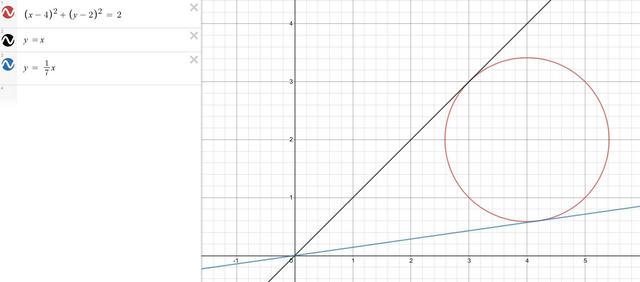
Ответ:
Уравнения касательных:
y = x
y = (1/7)*x
Объяснение:
Решение на рисунке.
Покажем, что т. A (3; 3) и т. B(4,2; 0,6) принадлежат как окружности, так и касаетльной.
(3 - 4)² + (3 - 2)² = 1 + 1 = 2, т.е. т. A на окружности.
Наклон графика (tan = 1) и наклон радиуса к tan = -1, т.е. радиус и касательная перпендикулятны.
(4,2 - 4)² + (0,6 - 2)² = 0,04 + 0,96 = 2
т. В лежит на окружности.
Наклон касательной tan = 1/7 и наклон радиуса tan = -7, т.е. радиус и касательная перпендикулярны.