Решите полностью, что указано на листке, даю 90 баллов!!!

1. Стороны относятся как 3:4:5, значит треугольник прямоугольный.

2. 5:2 = 2,5 коэффициент подобия.

Отношение площадей равно квадрату коэффициента подобия.

S2 = 8·(2,5)² = 8·6,25 = 50 см².

3. $r=\frac b2\sqrt{\frac{2a-b}{2a+b}},$ где a - боковая сторона, b - основание.

$P=2a+b\Rightarrow a=\frac{P-b}2=\frac{32-12}2=\frac{20}2=10$ см боковая сторона.

$r=\frac{12}2\sqrt{\frac{2\cdot10-12}{2\cdot10+12}}=6\sqrt{\frac{20-12}{20+12}}=6\sqrt{\frac8{32}}=6\sqrt{\frac14}=6\cdot\frac12=3$ см.

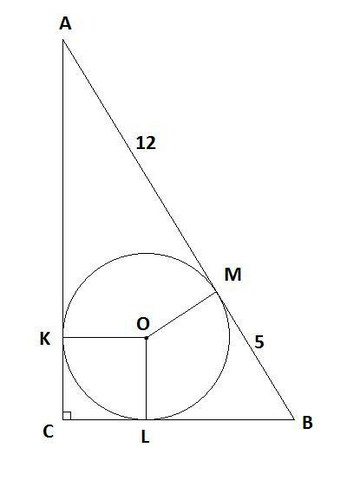
4. Пусть радиус вписанной окружности r см. OK = OL = OM = r (см. рис.).

Угол C прямой по условию, углы OKC и OLC равны, т.к. радиус, опущенный к точке касания, перпендикулярен касательной. Значит OKCL - прямоугольник.

Более того, OK = OL как радиусы, значит OKLC - квадрат.

AK = AM = 12 см, т.к. это касательные, проведённые из одной точки А.

BL = BM = 5 см, т.к. это касательные, проведённые из одной точки B.

Значит AC = AK+KC = 12+r, BC = BL+LC = 5+r.

По теореме Пифагора

$AC^2+BC^2=AB^2\\\\(12+r)^2+(5+r)^2=(17)^2\\144+24r+r^2+25+10r+r^2=289\\2r^2+34r-120=0\;\;\;\div2\\r^2+17r-60=0\\D=(17)^2-4\cdot1\cdot(-60)=289+240=529\\r_{1,2}=\frac{-17\pm23}2\\r_1=-20\;-\;He\;nogx.\\r_2=3$

r = 3 см, тогда

AC = 12+3 = 15 см

BC = 5+3 = 8 см.

5. $R=\frac12\sqrt{a^2+k^2}$

Решите полностью, что указано ** листке, даю 90 баллов!!!