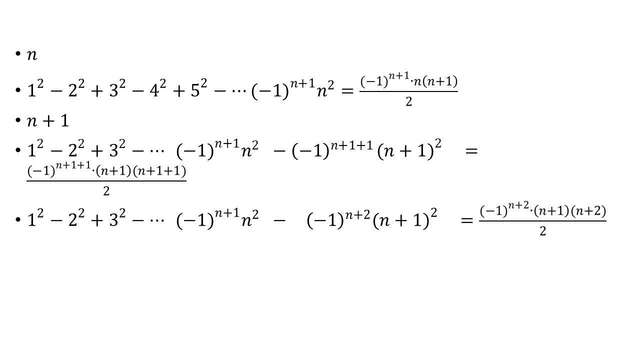Условие и вопрос ** рисунке!!!

Question

Условие и вопрос на рисунке!!!

---

Comments

Не моя тема, извини)

---

этого надо решить?

---

я решу, подожди, щас времени нет

---

не успел загрузить, меня опередили

Answer 1

Ответ:

Объяснение:

Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел.

 Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.                                  

Answer 2

znanija.com/task/36577873

Используя  метод математической индукции  докажите следующее утверждение 1² - 2² +3²- 4² +5 ²- 6²+ ...(-1)ⁿ ⁺¹*n²=(-1)ⁿ ⁺¹ *n(n+1)/2.

Объяснение:

1² - 2² +3²- 4² +5 ²- 6²+ ...(-1)ⁿ ⁺¹*n²=(-1)ⁿ ⁺¹ *n(n+1)/2.

1. n =1  верно   действительно   (-1)¹ ⁺¹*1²= 1     и     (-1)¹ ⁺¹*1(1+1)/2 = 1.

2. допустим верно при n =k   т.е.

1² - 2² +3²- 4² +5 ²- 6²+ ...(-1)^(k+1)*k² = (-1)^(k+1)  * k(k+1)/2.

3. докажем верно и при n =k+1

1² - 2² +3²- 4² +5 ²- 6²+ ...(-1)^(k+1)*k² ....(-1)^(k+2)*(k+1)²  =

(-1)^(k+1)  * k(k+1)/2 + (-1)^(k+1+1 )*(k+1)² =(-1)^(k+1) *( (k(k+1)/2 - (k+1)² ) =

(-1)^(k+1) *( (k(k+1) -2(k+1)² ) /2 =(-1)^(k+1) *( k²+k -2k²-4k-2 ) /2 =

(-1)^(k+1) *( - k²-3k  -2 ) /2  =(-1)^(k+2) *(  k²+3k +2 ) /2  =

(-1)^(k+2) *(k+1)(k+2) /2    сохранил  свой вид  → утверждение верно

---

---