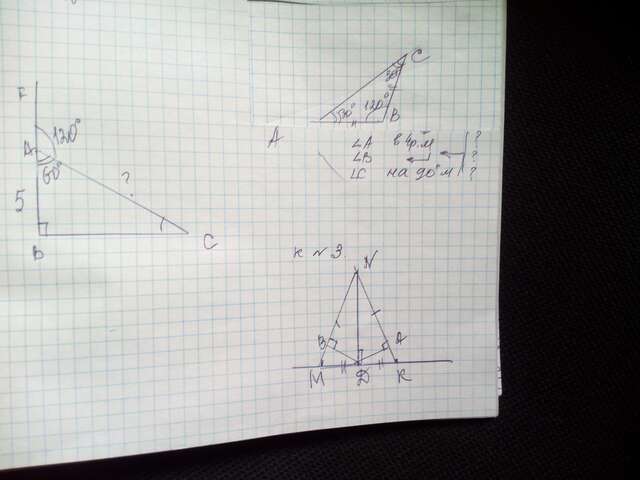Угол А равен х, угол В 4х, угол С =4х-90, сумма углов в треугольнике равна 180, поэтому х+4х+4х-90=180, 9х=270, х=30
Значит, ∠А=30°;∠В=4*30°=120°; ∠С=120°-90°=30°- АВ, значит, углы при основании АС в треугольнике равны, значит, он равнобедренный по признаку равнобедренного треугольника, тогда АВ =ВС.
2. Внутренний с углом внешним при вершине А угол равен 60°, т.к. их сумма 180°. тогда другой острый угол С равен 30°, против него лежит катет АВ, который равен половине гипотенузы, значит, гипотенуза равна 5*2=10/см/
3. Т.к. МК- основание равнобедренного треугольника MNK, и по условию ND- медиана, но тогда она является и высотой в данном треугольнике, MK⊥ND и биссектрисой , все точки которой равноудалены от сторон угла, т.е. DN=DA, что и требовалось доказать. Как говорил Евклид.)