В равнобедренном треугольнике боковые стороны равны 15 см,а высота опущенная ** основание...

Question

В равнобедренном треугольнике боковые стороны равны 15 см,а высота опущенная на основание равна 12 см.Найдите радиус описанной около треугольника окружности?

с подробным решением

Answer 1

В принципе я согласна с предложенным ответом, в решение не всматривалась

 Сейчас предложу своё. Рисунок позже нарисую

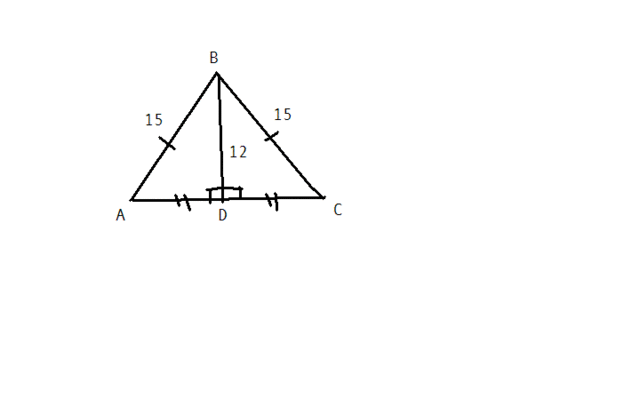
Так как AD высота равнобедренного треугольника, то по сойству она тявляется медианой.

 Рассмотрим прямоугольный треугольник ABD по теореме Пифагора найдём катет AD

AD =√AB^2-BD^2=√225-144=√81=9

 Так как AD медиана, то  AC=18

 Площадь произвольного треугольника S=1/2*АС*BD=1/2*12*18=108

Радиус описанной окружности произвольного треугольника вычисляется по формуле

R=(AB*BC*AC)/4S=(15*15*15)/(4*108)=9.375

---

Answer 2

Радиус описанной окружности вычисляется по формуле R=abc/4S, где abc - стороны треугольника, S - его площадь. Площадь равнобедренного треугольника S=1/2bh, где и - основание, к которму проведена высота и h - высота. Итак, треугольник ABC с высотой BO. Найдем AC. AB²=BO²+AO² по теореме Пифагора. 225=144+AO²

AO²=81, AO=9. Так как AO=OC, то 9*2=18=AC

Находим площадь треугольника

1/2*18*12=108

Находим радиус 15*15*18/4*108=4050/432=9,375