Ответ:
S полн. пов=25√3 см^2
высота тетраэдра Н=(5/3)√6 см
Объяснение:
тетраэдр - правильный многогранник все грани, которого правильные треугольники, их 4.
1. S полн. пов=4×S∆
площадь правильного треугольника:

площадь полной поверхности:
S=25√3 см^2
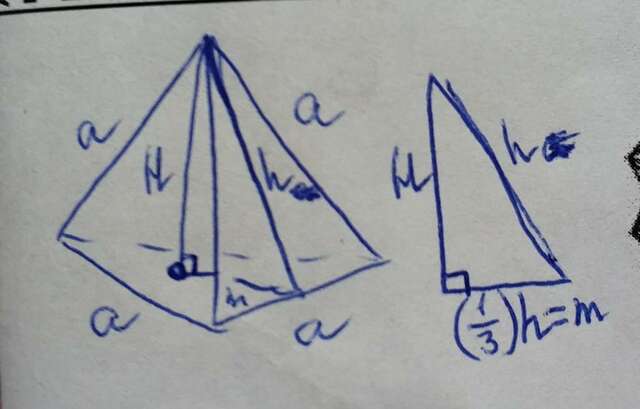
2. рассмотрим прямоугольный треугольник
гипотенуза h - высота боковой грани тетраэдра - высота правильного треугольника

катет m -(1/3) высота основания тетраэдра - высоты правильного треугольника

катет Н - высота тетраэдра, найти по теореме Пифагора:
Н^2=h^2-m^2

высота тетраэдра Н