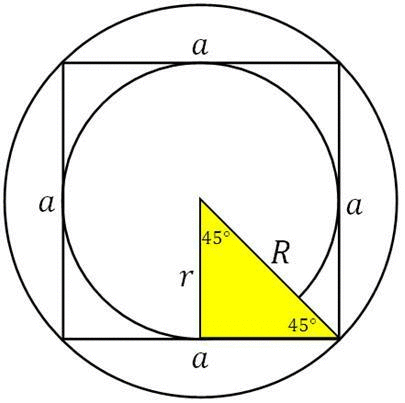
Задача: Радиус окружности, описанной около квадрата, равен 26√2. Найти радиус окружности, вписанной в этот квадрат.
Решение:
Радиус окружности, описанной около квадрата, (R) равен полудиагонали этого квадрата, то есть вся диагональ (d) равна:
d = 2R = 2*26√2=52√2
Используя т. Пифагора, найдем длину стороны (a) квадрата:

(отрицательное значение отбрасывает — не подходит по условию задачи)
Радиус окружности, вписанной в этот квадрат, (r) равен половине его стороны:

Ответ: Радиус окружности, вписанной в квадрат, равен 26.