Ответ:
a) Sп = 450 см²
б) Sс ≈ 89,67 см²
Объяснение:
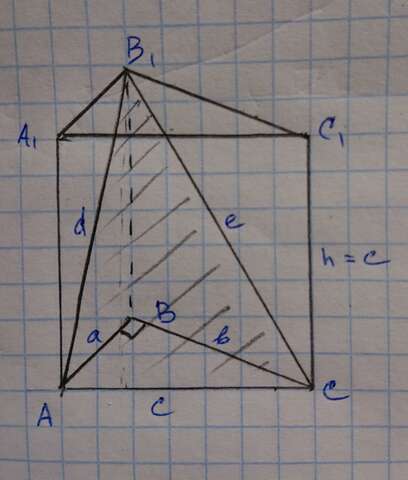
см. рисунок
пусть AB = a = 5 см
BC = b = 12 см
AC = c = √(a² + b²) - т. Пифагора
с = √(25 + 144) = √169 = 13 см
Наибольшая грань ACC1A1 => h = c = 13 см
a)
Площадь полной поверхности
S = 2*(1/2)*ab + a*c + b*c + c*c = ab + c(a+b+c) = 60 + 13(30) = 450 см²
б)
Найдём боковые стороны сечения
d = √(a² + c²) = √194
e = √(b² + c²) = √313
S = √(p(p - d)(p - e)(p - c))
где p - полупериметр
p = (d + e + c)/2 = (√194 + √313 + 13)/2 ≈ (13,93 + 17,69 + 13)/2 = 22,31
S ≈ √(22,31*8,38*4,62*9,31) = 89,67 см²
P.S. если a) = решение красивое, то б) какое-то долгое и на вычисление. Это несколько настораживает.