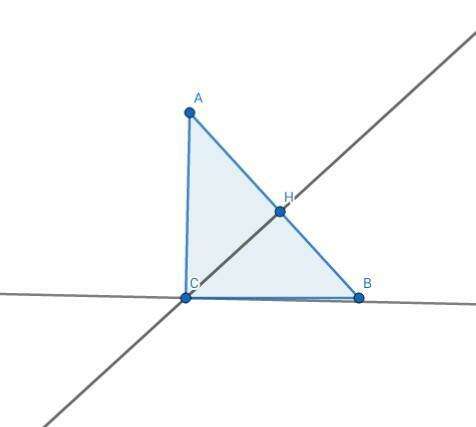
Дано:
∆ABC - прямоугольный.
∠C = 90°
∠B = 30°
AB = 36 см.
CH - высота.
Найти:
BH.
Решение.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> AC = 18 см.
Сумма острых углов прямоугольного треугольника равняется 90°
=> ∠CAB = 90 - 30 = 60°
=> ∠ACH = 90 - 60 = 30°
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> AH = 9 см.
BH = 36 - 9 = 27 см.
Ответ: 27 см.