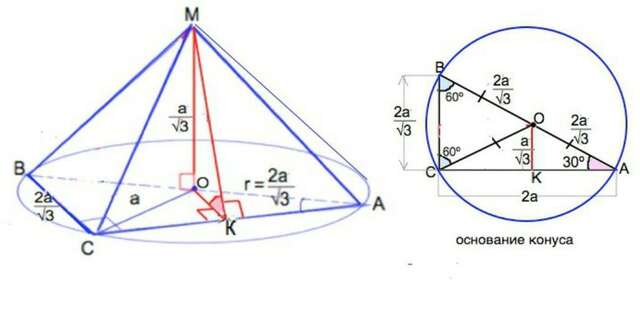
Нужно сначала найти радиус основания конуса.
Основание пирамиды - прямоугольный треугольник. Значит радиус основания конуса, как описанной окружности, равен половине гипотенузы вписанного треугольника.
Пусть это ∆ АВС∠С=90º∠А=30º
АС=2а
ГипотенузаАВ=АС:cos 30º=4a÷√3
R=АО=ВО=ОС=2a÷√3
Катет - ВС=2a÷√3 как противолежащий углу 30º
Угол между боковой гранью и плоскостью основания равен углу между перпендикулярами. Проведенными к точке О и М из точки К катета АС (МК - наклонная, ОК - ее проекция, МК и ОК перпендикулярны АС по т. о трех перпендикулярах). К - середина основания АС равнобедренного ∆ АОС
Так как угол ОКА=90º, ОК|| ВС и является средней линией ∆ АВС и равна половине ВС.
ОК=ВС:2=а/√3
Высота пирамиды МО перпендикулярна плоскости основания, угол МКО=45º по условию, и ∆ МОК - равнобедренный. МО=ОК=а÷√3
S осн. конуса=πR²=4π•a²÷3
V=[(4π•а²÷3)•a÷√3]:3=4π•a³÷√3 (ед. объема)
(изображение взято из других работ)