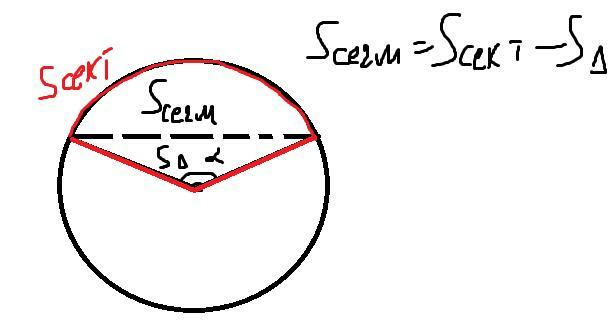
В общем случае площадь сегмента находится как разность площади соответствующего ему сектора круга и площади треугольника, который как бы "вырезается из сектора", т.е.  сегм =
сегм =  сект -
сект -  .
.
Площадь сектора находится по формуле
 сект =
сект =  , где R - собственно, радиус, α - центральный угол, равный величине соответствующей дуги.
, где R - собственно, радиус, α - центральный угол, равный величине соответствующей дуги.
С учетом формулы  , где a и b - стороны, α - угол между ними, в данном случае площадь треугольника равна
, где a и b - стороны, α - угол между ними, в данном случае площадь треугольника равна
 (т.к. треугольник равнобедренный и его стороны равны радиусу).
(т.к. треугольник равнобедренный и его стороны равны радиусу).
Тогда  сегм =
сегм =  .
.
Подставляем:
1) Sсегм = 
2) Sсегм = 
3) Sсегм =