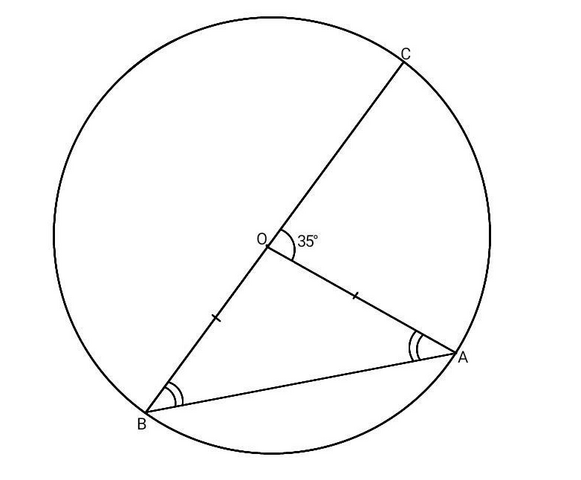
Дано:
Окружность с центром О.
ВС - диаметр.
А Є окружности.
Угол АОС = 35°.
Найти:
Угол ВАС = ?
Решение:
Рассмотрим ∆ВОА - равнобедренный (так как ВО = ОА - радиусы одной окружности). Тогда углы ВАО = ОВА (по свойству равнобедренного треугольника). Угол СОА - внешний для ∆ВОА => угол СОА = угол ВАО + угол ОВА => угол ВАО в два раза меньше угла СОА => Угол ВАО = 35°:2 = 17,5°.
Ответ: 17,5°.